先讲回归这个概念,我的理解:如果是二维平面里,指根据现有的点拟合出直线,在用直线做分析与预测。
简单线性回归便是全部的点都在一类之下。拟合出直线用于发现其中的关系。
logistic回归是在两类里做分类,完成训练后,拟合出的直线一边各一类,新来的点就可以很轻易的分类。
softmax回归便是多分类。
然后用python进行了尝试
#python2.7 import numpy as np import matplotlib.pyplot as plt num=1000 vectors=[] xx=0;xy=0;ex=0;ey=0 for i in xrange(num): x1=np.random.normal(0.0,0.55) y1=x1*0.1+0.3+np.random.normal(0.0,0.03) xx+=x1*x1 xy+=x1*y1 ex+=x1 ey+=y1 vectors.append([x1,y1]) x_data=[v[0] for v in vectors] y_data=[v[1] for v in vectors] plt.plot(x_data,y_data,'ro',label='data') b=(xy-ex*ey/num)/(xx-ex*ex/num) a=ey/num-b*ex/num tmpx=[-2,0,2] tmpy=[] for i in tmpx: tmpy.append(b*i+a) plt.plot(tmpx,tmpy) plt.legend() plt.show()
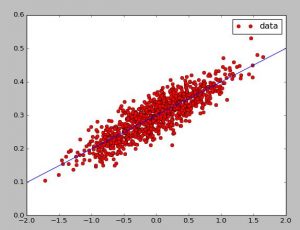
效果还可以,之后会对回归进行更多的优化和尝试,最小二乘法,梯度下降等等
版权声明:本文为原创文章,转载请注明出处和作者,不得用于商业用途,请遵守
CC BY-NC-SA 4.0协议。
赞赏一下

 支付宝打赏
支付宝打赏 微信打赏
微信打赏