刚开始理解svm(支持向量机)还是挺复杂的,现在稍微有了一点思路,便写下来。由于代码实现中对于svm基本是黑盒,所以这里直接讲一下,再用代码实现。
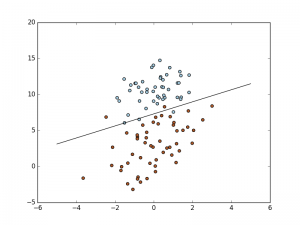
在线性的情况下,svm就直接找一个超平面(下面就是那条线)来分割不同的两类。比如这个二分类,在超平面上的点距离这条线为0,定一侧距离这条线为正,一侧距离这条线为负,那么只要找到两类点和超平面最大的距离和就行。
#python2.7
#coding:utf-8
#引入所需库
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
#点集和类别
f=open("testSet.txt")
data=[]
label=[]
#取点
for i in f.readlines():
linearr=i.strip().split()
data.append([float(linearr[0]),float(linearr[1])])
label.append(int(linearr[2]))
data=np.array(data)
#建立线性模型
clf = svm.SVC(kernel='linear')
#训练
clf.fit(data, label)
#取到训练完的权值
w = clf.coef_[0]
a = -w[0] / w[1]
#设定x坐标
xx = np.linspace(-5, 5)
#根据权值求得y
yy = a * xx - (clf.intercept_[0]) / w[1]
#画直线
plt.plot(xx, yy, 'k-')
#画点集
plt.scatter(data[:, 0], data[:, 1], s=30, c=label, cmap=plt.cm.Paired)
plt.show()
对于非线性的情况,个人简单的理解:如果在一维没法分类解决的问题,就放到二维去解决,同理,二维可以用三维解决。
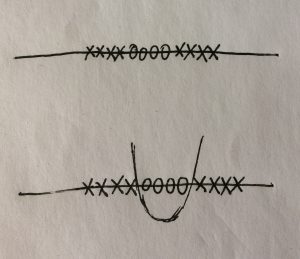
例:下图中,圈是一类,叉是另一类。在一维点集里,没法用一个点来分别两个类别。所以升维到二维后,就发现很简单的用一条曲线就做好了分类。而找这条曲线或曲面首先就需要一个核函数。
#python2.7 #coding:utf-8 #引入所需库 import numpy as np import matplotlib.pyplot as plt from sklearn import svm #这个文件创建方式点击这里 f=open("testSet2.txt") data=[] label=[] #定义250000个点的二维点集 xx,yy=np.meshgrid(np.linspace(-3, 3, 500),np.linspace(-3, 3, 500)) #读取点 for i in f.readlines(): linearr=i.strip().split() data.append([float(linearr[0]),float(linearr[1])]) label.append(int(linearr[2])) data=np.array(data) #建立模型,核函数默认 clf = svm.SVC() #训练数据 clf.fit(data, label) #根据250000个点得到距离超平面距离 Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()]) #结果转为二维 Z = Z.reshape(xx.shape) #画出平面上距离超平面为0的轮廓 contours = plt.contour(xx, yy, Z, levels=[0], linewidths=2,linetypes='--') #画点集 plt.scatter(data[:, 0], data[:, 1], s=30, c=label, cmap=plt.cm.Paired) plt.show()
结果展示: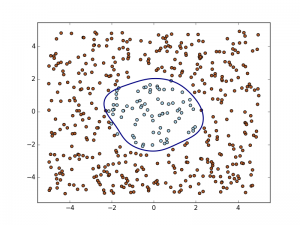
版权声明:本文为原创文章,转载请注明出处和作者,不得用于商业用途,请遵守
CC BY-NC-SA 4.0协议。
赞赏一下
 支付宝打赏
支付宝打赏 微信打赏
微信打赏