之前讲过最简单的线性拟合和逻辑回归,但常常的情况并不是一条直线就能解决问题的,所以来研究一下非线性的。
总体方法还是和之前差不多的,只是改变了初始的变量的指数。首先列出式子,求cost function(代价函数,一般理解就是拟合的线与实际的点差多少距离经过处理的总和)。在根据梯度下降最小化cost function,就可以求得接近点的一组系数解,也就是下面的θ,之后就得到直线了。
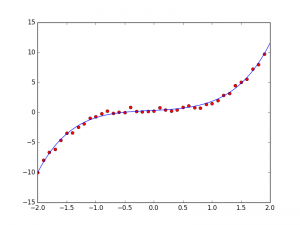
先来看非线性拟合,这里还是用for而不是矩阵来实现中间一些计算。
#python2.7
#coding:utf-8
#引入相关库
import numpy as np
import matplotlib.pyplot as plt
#模拟产生点坐标
k=int(np.random.random()*5+1)
x=np.arange(-2,2,0.1)
y=0
for i in range(k):
y+=np.random.random()*(x**k)
y+=np.random.random(len(x))
#N--幂指数也就是最高x^6
#这里可以改进,如果N再高计算中会出现nan
N=6
#这个矩阵为上面的θ
A=np.array([1]*N)
#点的数量
l=len(x)
#梯度下降步长
alpha=0.01
#进行一千次迭代
for _ in xrange(1000):
#z为cost function叠加的那部分和的矩阵
z=np.zeros(N)
#遍历每个点,计算代价和
for i in xrange(l):
sh=0
for j in xrange(N):
sh+=A[j]*x[i]**j
for m in xrange(N):
z[m]+=(sh-y[i])*x[i]**m
#直接用矩阵计算更新所有θ
A=A-alpha*z/l
#下面为画图部分
plt.plot(x,y,"ro")
tmpx=np.linspace(-2,2)
def cal(x):
tmpy=0
for i in xrange(N):
tmpy+=A[i]*x**i
return tmpy
tmpy=[cal(tmpx[i]) for i in range(len(tmpx))]
plt.plot(tmpx,tmpy)
plt.show()
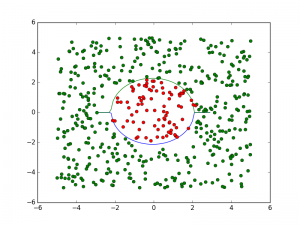
再来看非线性logistic回归。

这里和上面主要改变的就是多了一步sigmoid函数,还有在求cost function的时候多了一步求ln,我发现比较可靠的一种理解是为了让函数为凸函数,梯度下降可以保证取到全局最低点。再求偏导得到更新θ的式子,基本是一样的。
#python2.7
#coding:utf-8
#产生点并写入文件
import numpy as np
f=open("testSet2.txt","w")
for i in xrange(500):
a=np.random.random()*5 if np.random.random()>0.5 else -np.random.random()*5
b=np.random.random()*5 if np.random.random()>0.5 else -np.random.random()*5
if a**2+b**2<5:
print >> f,str(a)+" "+str(b)+" 0"
else:
print >> f,str(a)+" "+str(b)+" 1"
#python2.7
#coding:utf-8
#引入相关库
import matplotlib.pyplot as plt
import numpy as np
#读取文件中的点坐标及分类
f=open("testSet2.txt")
#两类点坐标
gdatax=[]
gdatay=[]
rdatax=[]
rdatay=[]
#类别
label=[]
#点坐标
data=[]
#代表有5个θ
N=5
#θ的矩阵
A=np.array([1]*N)
#步长,这里设的比较大因为小了到不了最低点
alpha=0.1
#不同类的点画不同颜色的点
for i in f.readlines():
linearr=i.strip().split()
data.append([float(linearr[0]),float(linearr[1])])
label.append(int(linearr[2]))
if int(linearr[2])==1:
gdatax.append(linearr[0])
gdatay.append(linearr[1])
else:
rdatax.append(linearr[0])
rdatay.append(linearr[1])
l=len(label)
#迭代2000次,过程和上面一样
for _ in xrange(2000):
z=np.zeros(N)
for i in xrange(l):
sh=1/(1+np.exp(-A[0]-data[i][0]*A[1]-data[i][1]*A[2]-A[3]*data[i][0]**2-A[4]*data[i][1]**2))
z[0]+=sh-label[i]
z[1]+=(sh-label[i])*data[i][0]
z[2]+=(sh-label[i])*data[i][1]
z[3]+=(sh-label[i])*data[i][0]**2
z[4]+=(sh-label[i])*data[i][1]**2
A=A-alpha*z/l
#下面为画图过程
tmpx=[i/10.0 for i in xrange(-30,30)]
tmpy=[]
tmpz=[]
for i in tmpx:
su=A[2]**2-4*A[4]*(A[0]+A[1]*i+A[3]*i**2)
if su<0:
tmpy.append(0)
tmpz.append(0)
else:
tmpy.append((-A[2]-np.sqrt(su))/(2*A[4]))
tmpz.append((-A[2]+np.sqrt(su))/(2*A[4]))
plt.plot(tmpx,tmpy)
plt.plot(tmpx,tmpz)
plt.plot(gdatax,gdatay,'ro',c='g')
plt.plot(rdatax,rdatay,'ro',c='r')
plt.show()
致谢:http://blog.csdn.net/abcjennifer/article/details/7716281
版权声明:本文为原创文章,转载请注明出处和作者,不得用于商业用途,请遵守
CC BY-NC-SA 4.0协议。
赞赏一下
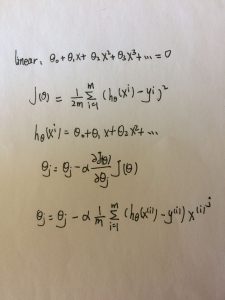
 支付宝打赏
支付宝打赏 微信打赏
微信打赏