一般的logistics回归过程并不复杂,特别是在理解了梯度下降之后,梯度下降法可以参考我之前的文章,点击这里查看
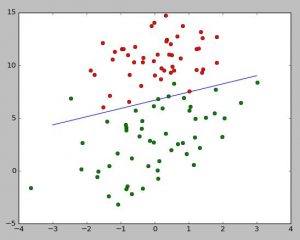
大致还是通过梯度下降把需要拟合的直线的前面的系数渐渐靠近,比如用ax+by+c=0,这条直线来进行二分类,a,b,c三个系数就是下面代码中的数组weight,每次迭代改变的就是weight。然后误差是通过把每组训练的数进行sigmoid函数 ![]() ,在与之前分好的类(这里是txt文件里的-1和1)进行求差就是每次的误差值。具体代码里还有解释。
,在与之前分好的类(这里是txt文件里的-1和1)进行求差就是每次的误差值。具体代码里还有解释。
"testSet.txt"是《机器学习实战》里的一个例子的文件,这里引用一下,下载地址在http://pan.baidu.com/s/1pLLMJdp
这个例子很考验矩阵运算,建议回顾一下线性代数哦!
#python2.7
#引入必要文件
import matplotlib.pyplot as plt
import numpy as np
#打开文件
f=open("testSet.txt")
gdatax=[]
gdatay=[]
rdatax=[]
rdatay=[]
label=[]
data=[]
#读取文件
for i in f.readlines():
#strip()是除去开头空格,split()是以空格为间断,变成数组。
linearr=i.strip().split()
#读取坐标,这里补1.0是为了使数组长度变成3,便于之后矩阵运算
data.append([1.0,float(linearr[0]),float(linearr[1])])
#读取分类
label.append(int(linearr[2]))
#为了展示点的分布,分开读取不同类的点
if int(linearr[2])==1:
gdatax.append(linearr[0])
gdatay.append(linearr[1])
else:
rdatax.append(linearr[0])
rdatay.append(linearr[1])
#使list变成numpy里的matrix矩阵
dataMatrix=np.mat(data)
#transpose()是矩阵的转置
labelMat=np.mat(label).transpose()
m,n=np.shape(dataMatrix)
#梯度下降步长
alpha=0.001
#梯度下降次数
max=500
#先设定三个系数为1
weights=np.ones((n,1))
#梯度下降主步骤,求sigmoid,和分类对比正确性,在求新的weights
for k in range(max):
h=1.0/(1+np.exp(-dataMatrix*weights))
error=(labelMat-h)
weights=weights+alpha*dataMatrix.transpose()*error
#创建等差数列
x=np.linspace(-3,3)
#计算y值
y=(-weights[0,0]-weights[1,0]*x)/weights[2,0]
#画图
plt.plot(x,y)
plt.plot(gdatax,gdatay,'ro',c='g')
plt.plot(rdatax,rdatay,'ro',c='r')
plt.show()
总的来说还可以。梯度下降那块可以优化成随机梯度下降,可以进行更少的迭代获得同等的效果。
版权声明:本文为原创文章,转载请注明出处和作者,不得用于商业用途,请遵守
CC BY-NC-SA 4.0协议。
赞赏一下
 支付宝打赏
支付宝打赏 微信打赏
微信打赏