梯度下降法:一般想法就是,开始先找一个点,之后每次找下降最快的那个方向来找下一个点,直到找到最低点。
看过很多教程或者高数书上的讲解,大致就知道梯度下降是怎么回事情。但很多时候都是被众多的公式和英文名词吓到而不真正理解。
这次我们来简单理解最初的一个------单变量梯度下降,这里用梯度下降来做线性回归,也就是找一条h(x)=ax+b的线来拟合现有的点。
想象有很多点,中间有条线,所有点不可能完全在线上,相对于线都有一个误差值,所以方程可以看做h(x)=ax+b+c(c代表差值),c=0就相当于点完全在线上。
之后再理解一个cost function的概念,看下面第二个式子,简单理解一下就是把所有c求了平方和再求平均,除以二是之后在偏导数的时候会方便点。
在下面求偏导就是把一式带入到二式然后求,结果如三四两式。那个α是步长也就是下降的快慢,过快或过慢都不好。这样算完就算一次下降,之后就反复进行就可以慢慢向需要的拟合回归线靠拢。
#python2.7 #产生点 import numpy as np import matplotlib.pyplot as plt x=np.arange(-2,2,0.1) y=2*x+np.random.random(len(x)) #随机设定一个初始的a,b a=np.random.random() b=np.random.random() l=len(x) #步长 alpha=0.01 #进行1000次梯度下降,每次计算出上面求出的偏导,并在赋值给a,b。 for _ in xrange(1000): j=0 k=0 for i in xrange(l): j+=(a*x[i]+b-y[i])*x[i] k+=a*x[i]+b-y[i] a=a-alpha*j/l b=b-alpha*k/l print a,b #画点 plt.plot(x,y,"ro") #画线 tmpx=np.linspace(-2,2) tmpy=tmpx*a+b plt.plot(tmpx,tmpy) plt.show()
效果展示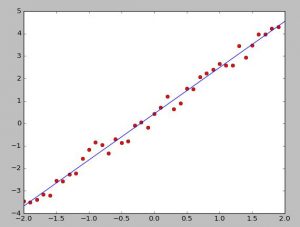
致谢:http://blog.csdn.net/abcjennifer/article/details/7691571
版权声明:本文为原创文章,转载请注明出处和作者,不得用于商业用途,请遵守
CC BY-NC-SA 4.0协议。
赞赏一下
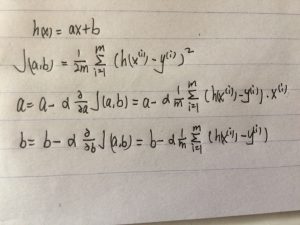
 支付宝打赏
支付宝打赏 微信打赏
微信打赏